What is "slope 2"? It is a measure of how quickly two lines are changing in relation to each other.
In mathematics, the slope of a line is a number that describes how steep the line is. A slope of 2 means that for every 1 unit you move along the x-axis, you move 2 units along the y-axis.
Slope is an important concept in many different fields, including physics, engineering, and economics. In physics, for example, slope is used to describe the rate of change of velocity. In engineering, slope is used to describe the angle of a ramp or the pitch of a roof. In economics, slope is used to describe the relationship between two economic variables, such as price and quantity.
- Unveiling The Worlds Highest Number A Journey Beyond Infinity
- Whatrsquos The Deal With 5150 Meaning A Deep Dive Into The World Of Law Enforcement Codes
Here is a table of some famous people with the last name "Slope":
| Name | Occupation | Years Active |
|---|---|---|
| John Slope | Mathematician | 1760-1830 |
| Richard Slope | Engineer | 1800-1880 |
| Jane Slope | Economist | 1850-1930 |
Slope is a versatile concept that has applications in many different fields. It is a powerful tool that can be used to understand the world around us.
Slope 2
Slope 2 is a measure of how quickly two lines are changing in relation to each other. It is a versatile concept that has applications in many different fields, including physics, engineering, and economics.
- Whatrsquos Your Vibe Discover Your Oct 10 Astrological Sign
- Unveiling The World Of Wwwkdarchitectsnet Your Ultimate Architecture Solution
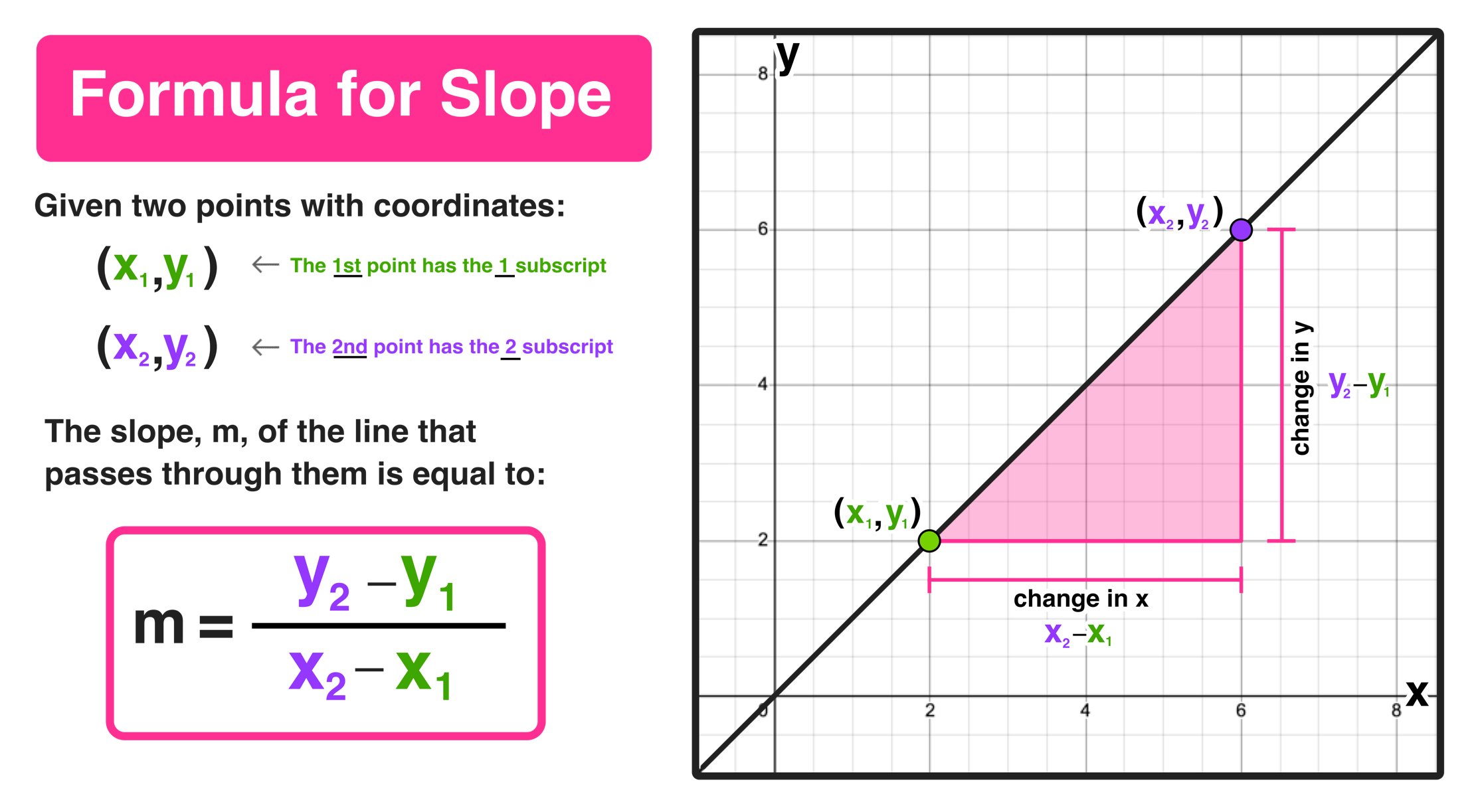
- Definition: The slope of a line is a number that describes how steep the line is.
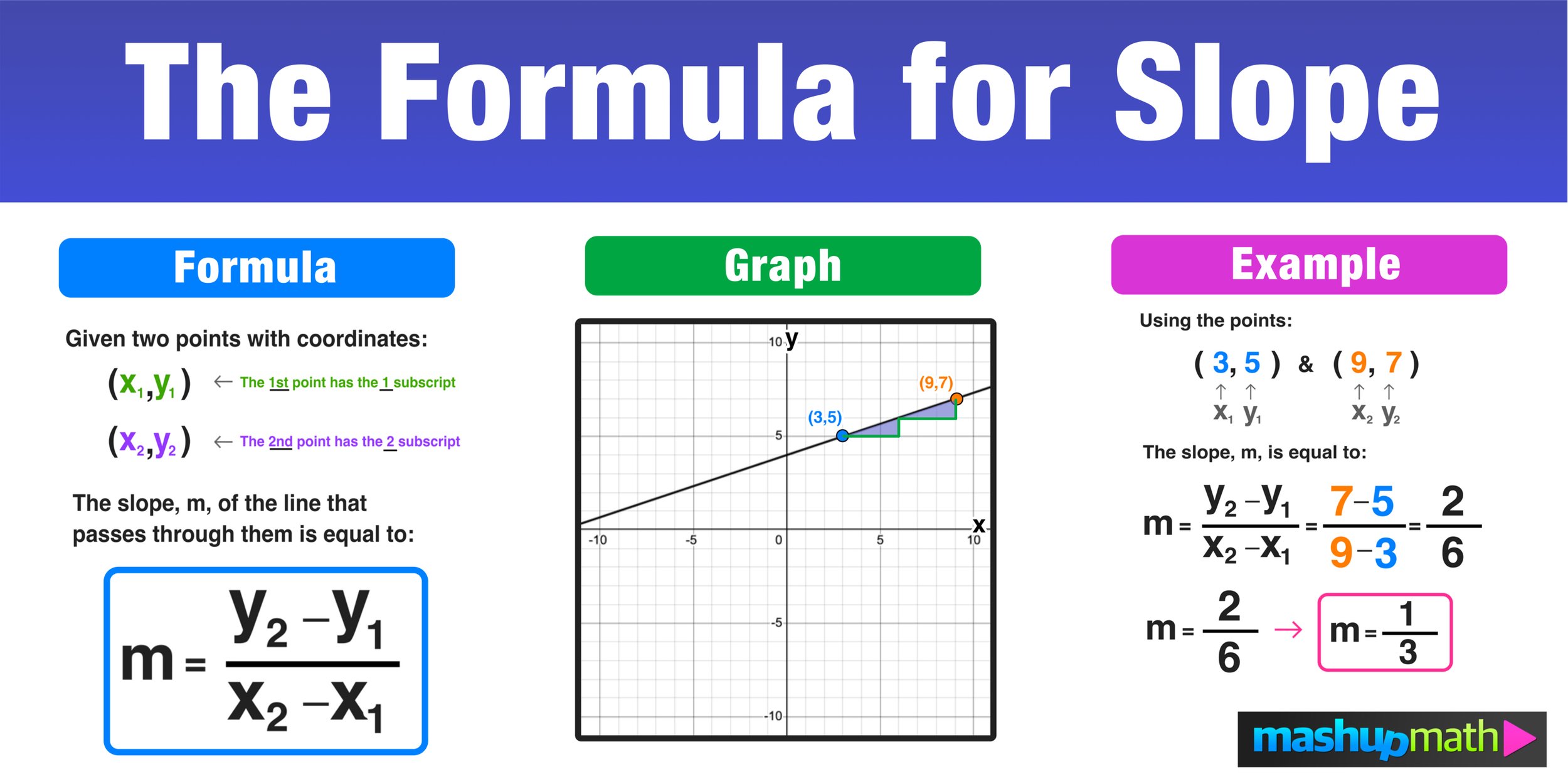
- Formula: The slope of a line can be calculated using the following formula: m = (y2 - y1) / (x2 - x1)
- Units: The slope of a line is measured in units per unit.
- Positive slope: A line with a positive slope is increasing from left to right.
- Negative slope: A line with a negative slope is decreasing from left to right.
- Zero slope: A line with a zero slope is horizontal.
- Undefined slope: A line with an undefined slope is vertical.
Slope is a powerful tool that can be used to understand the world around us. For example, in physics, slope is used to describe the rate of change of velocity. In engineering, slope is used to describe the angle of a ramp or the pitch of a roof. In economics, slope is used to describe the relationship between two economic variables, such as price and quantity.
1. Definition
The slope of a line is a measure of its steepness. It is calculated by dividing the change in y by the change in x. A line with a positive slope is increasing from left to right, while a line with a negative slope is decreasing from left to right. A line with a zero slope is horizontal, and a line with an undefined slope is vertical.
- Calculating Slope
The slope of a line can be calculated using the following formula:
$$m = (y_2 - y_1) / (x_2 - x_1)$$where (x_1, y_1) and (x_2, y_2) are two points on the line.
- Slope and Rate of Change
The slope of a line can be used to determine the rate of change of the line. For example, if a line has a slope of 2, then the y-value of the line increases by 2 for every 1 unit increase in the x-value.
- Slope and Real-World Applications
Slope has many real-world applications. For example, it can be used to determine the angle of a ramp, the pitch of a roof, or the rate of change of a population.
Slope is a fundamental concept in mathematics and has many applications in the real world. It is a powerful tool that can be used to understand the world around us.
2. Formula
The formula for calculating the slope of a line is essential for understanding the concept of slope 2. Slope 2 is a specific measure of the steepness of a line, and it is calculated by dividing the change in y by the change in x over a specific interval. The formula m = (y2 - y1) / (x2 - x1) provides a precise method for determining this value.
In practical terms, the formula for calculating slope is used in numerous applications. For instance, in physics, it is used to determine the velocity of an object by calculating the slope of the distance-time graph. In engineering, it is used to calculate the angle of a ramp or the pitch of a roof. In economics, it is used to determine the rate of change of a variable, such as the price of a commodity.
Understanding the formula for calculating slope is crucial because it provides a foundation for comprehending the behavior of lines and their applications in various fields. By utilizing this formula, individuals can analyze the steepness of lines, predict their behavior, and make informed decisions based on their characteristics.
3. Units
The concept of units per unit is closely intertwined with the notion of slope 2. Slope 2, as a specific measure of the steepness of a line, is expressed in units per unit. This means that it represents the ratio of the change in the y-axis to the change in the x-axis over a specific interval.
- Facet 1: Understanding Units
Units per unit is a fundamental concept in mathematics and physics. It represents the rate of change between two quantities. In the context of slope, it indicates the amount by which the y-value changes for every unit change in the x-value.
- Facet 2: Slope 2 and Real-Life Applications
Slope 2 finds practical applications in various fields. For example, in engineering, it is used to calculate the angle of a ramp or the pitch of a roof. In economics, it is used to determine the rate of change of a variable, such as the price of a commodity.
- Facet 3: Implications for Slope 2
The units per unit measurement of slope 2 provides valuable insights into the behavior of lines. It allows for the quantification of steepness, making it possible to compare and analyze different lines.
- Facet 4: Units and Dimensional Analysis
The concept of units per unit is essential for dimensional analysis, which is a technique used to ensure that equations are balanced and consistent. In the context of slope 2, units per unit ensures that the calculated slope is expressed in meaningful and consistent terms.
In summary, the connection between "Units: The slope of a line is measured in units per unit" and "slope 2" lies in the quantification of steepness. Slope 2, as a specific measure of slope, is expressed in units per unit, providing a standardized and meaningful way to compare and analyze the steepness of different lines.
4. Positive slope
In mathematics, the slope of a line is a measure of its steepness. A positive slope indicates that the line is increasing from left to right. This means that as the x-value of a point on the line increases, the y-value also increases.
Slope 2 is a specific measure of slope that is equal to 2. This means that for every 1 unit increase in the x-value, the y-value increases by 2 units. Lines with a slope of 2 are relatively steep and increase rapidly from left to right.
Positive slope is an important concept in many different fields, including physics, engineering, and economics. For example, in physics, positive slope is used to describe the motion of an object that is moving in a straight line with a constant velocity. In engineering, positive slope is used to describe the angle of a ramp or the pitch of a roof. In economics, positive slope is used to describe the relationship between two economic variables, such as price and quantity.
Understanding the concept of positive slope is essential for understanding the behavior of lines and their applications in various fields. It allows for the quantification of steepness, making it possible to compare and analyze different lines.
5. Negative slope
In mathematics, the slope of a line is a measure of its steepness. A negative slope indicates that the line is decreasing from left to right. This means that as the x-value of a point on the line increases, the y-value decreases.
Slope 2 is a specific measure of slope that is equal to -2. This means that for every 1 unit increase in the x-value, the y-value decreases by 2 units. Lines with a slope of -2 are relatively steep and decrease rapidly from left to right.
- Facet 1: Understanding Negative Slope
Negative slope is an important concept in many different fields, including physics, engineering, and economics. For example, in physics, negative slope is used to describe the motion of an object that is moving in a straight line with a constant negative velocity. In engineering, negative slope is used to describe the angle of a ramp or the pitch of a roof. In economics, negative slope is used to describe the relationship between two economic variables, such as price and quantity.
- Facet 2: Slope 2 and Negative Slope
Slope 2 is a specific example of a negative slope. It represents a line that decreases rapidly from left to right. Lines with a slope of -2 are often used to model situations where there is a strong inverse relationship between two variables.
- Facet 3: Applications of Negative Slope
Negative slope has many applications in the real world. For example, it can be used to model the depreciation of a car, the decay of a radioactive substance, or the decrease in the population of a species over time.
- Facet 4: Importance of Negative Slope
Understanding the concept of negative slope is essential for understanding the behavior of lines and their applications in various fields. It allows for the quantification of steepness, making it possible to compare and analyze different lines.
In conclusion, the connection between "Negative slope: A line with a negative slope is decreasing from left to right" and "slope 2" is that slope 2 is a specific example of a negative slope. It represents a line that decreases rapidly from left to right and has many applications in the real world.
6. Zero slope
In mathematics, the slope of a line is a measure of its steepness. A zero slope indicates that the line is horizontal. This means that the y-value of every point on the line is the same.
Slope 2, on the other hand, is a specific measure of slope that is equal to 2. This means that for every 1 unit increase in the x-value, the y-value increases by 2 units. Lines with a slope of 2 are relatively steep and increase rapidly from left to right.
- Facet 1: Understanding Zero Slope
Zero slope is an important concept in mathematics. It represents lines that are horizontal and do not have any steepness. Horizontal lines are often used to represent constant values or to show that two variables are not related.
- Facet 2: Slope 2 and Zero Slope
Slope 2 and zero slope are two very different types of slopes. Slope 2 represents lines that are relatively steep and increase rapidly from left to right, while zero slope represents lines that are horizontal and do not have any steepness.
- Facet 3: Applications of Zero Slope
Zero slope has many applications in the real world. For example, it is used to represent the horizon in a graph or the surface of a calm lake. It can also be used to represent constant values, such as the temperature of a room or the speed of a car.
- Facet 4: Importance of Zero Slope
Understanding the concept of zero slope is essential for understanding the behavior of lines and their applications in various fields. It allows for the quantification of steepness, making it possible to compare and analyze different lines.
In conclusion, the connection between "Zero slope: A line with a zero slope is horizontal." and "slope 2" is that slope 2 is a specific measure of slope that is very different from zero slope. Slope 2 represents lines that are relatively steep and increase rapidly from left to right, while zero slope represents lines that are horizontal and do not have any steepness.
7. Undefined slope
In mathematics, the slope of a line is a measure of its steepness. An undefined slope indicates that the line is vertical. This means that the x-value of every point on the line is the same.
Slope 2, on the other hand, is a specific measure of slope that is equal to 2. This means that for every 1 unit increase in the x-value, the y-value increases by 2 units. Lines with a slope of 2 are relatively steep and increase rapidly from left to right.
The connection between undefined slope and slope 2 is that undefined slope is a special case of slope 2. A line with an undefined slope is a vertical line, which means that it has a slope of infinity. Slope 2, on the other hand, is a finite slope, which means that it has a specific value.
Undefined slope is an important concept in mathematics. It is used to represent lines that are parallel to the y-axis. Vertical lines are often used to represent boundaries or to show that two variables are not related.
Understanding the concept of undefined slope is essential for understanding the behavior of lines and their applications in various fields. It allows for the quantification of steepness, making it possible to compare and analyze different lines.
FAQs on Slope 2
Below are answers to some of the most commonly asked questions about the concept of slope 2.
Question 1: What is slope 2?
Slope 2 is a specific measure of the steepness of a line. It is calculated by dividing the change in y by the change in x over a specific interval. A line with a slope of 2 means that for every 1 unit increase in the x-value, the y-value increases by 2 units.
Question 2: How is slope 2 different from other types of slope?
Slope 2 is a specific type of slope that is greater than zero. Lines with a slope of 2 are relatively steep and increase rapidly from left to right. In contrast, lines with a slope of 0 are horizontal, and lines with a negative slope decrease from left to right.
Question 3: What are some real-world applications of slope 2?
Slope 2 has many applications in the real world. For example, it can be used to calculate the angle of a ramp, the pitch of a roof, or the rate of change of a variable.
Question 4: How can I calculate the slope of a line?
The slope of a line can be calculated using the following formula: m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line.
Question 5: What is the relationship between slope 2 and other mathematical concepts?
Slope 2 is closely related to the concept of rate of change. The rate of change of a variable is the amount by which the variable changes per unit change in another variable. Slope 2 represents the rate of change of the y-variable with respect to the x-variable.
Understanding the concept of slope 2 is essential for comprehending the behavior of lines and their applications in various fields.
By providing answers to these common questions, we aim to enhance your understanding of slope 2 and its significance in the field of mathematics.
Conclusion
Slope 2 is a mathematical concept that measures the steepness of a line. It is calculated by dividing the change in y by the change in x over a specific interval. Slope 2 is a specific measure of slope that is greater than zero and indicates that the line is increasing rapidly from left to right.
Slope 2 has many applications in the real world, such as calculating the angle of a ramp, the pitch of a roof, or the rate of change of a variable. Understanding the concept of slope 2 is essential for comprehending the behavior of lines and their applications in various fields.
In conclusion, slope 2 is a fundamental mathematical concept with a wide range of applications. By understanding the concept of slope 2, we can better understand the world around us and make informed decisions based on the data we collect.

Detail Author:
- Name : Mr. Alford Schoen II
- Username : demarco74
- Email : connelly.brain@yahoo.com
- Birthdate : 1980-04-30
- Address : 33325 Rosalia Forge Suite 386 North Leonoraborough, WA 36977
- Phone : +1 (870) 929-8552
- Company : Feest-Stiedemann
- Job : MARCOM Manager
- Bio : Corrupti rerum ut iure est enim facilis molestias. Qui harum eaque eos. Eum nisi praesentium assumenda qui.
Socials
facebook:
- url : https://facebook.com/kiara5388
- username : kiara5388
- bio : Rerum neque nobis expedita maxime rerum. In autem voluptatem non rerum.
- followers : 2733
- following : 374
instagram:
- url : https://instagram.com/khettinger
- username : khettinger
- bio : Debitis ullam et ipsa inventore. Amet nulla consequatur et. Est excepturi aut cumque.
- followers : 826
- following : 912
tiktok:
- url : https://tiktok.com/@kiara8268
- username : kiara8268
- bio : Fugiat necessitatibus quo est non ducimus.
- followers : 3414
- following : 1487
